TRCP-HOME > ロボット部 > 活動レポート・活動実績 > 詳細
2012年6月27日
6月24日(日)に行われた、レゴエデュケーション主催「レゴエデュケーションカンファレンス2012」において、9〜12年生数学科・ロボット部顧問の横山絢美教諭が、「レゴブロック授業アイデアコンテスト」特別賞に選ばれました。
初めて日本で開催されたこのコンテストは、レゴでロボットを作るのではなく、従来からあるレゴブロック約30個を利用し、授業に活かすアイデア授業案(学年、教科、設定時間を問わない)を募集したものです。対象は、学校従事者および教職員とされています。
5月中、コンテストへの応募が行われ、その結果が6月24日に発表されました。初年度となる今年、全体で100件以上にもおよぶ授業案の応募がありました。審査方法は、「ブラインドスタイル」という応募者の名前を隠した方法で行われました。
この「特別賞」は第3位に位置づけされ、受賞した2名の一人が、横山絢美教諭となりました。
「レゴエデュケーションカンファレンス」は、生徒たちが科学技術に興味関心をもち、ものづくりの楽しさを感じるきっかけとなることを目標とし、教職員のモチベーション向上やスキルアップにつながる場として設けられています。
ワークショップでは、ロボット製作をとおしてプレゼンテーション力、思考力、想像力、企画力などを養うための体験型授業に参加をしたり、レゴブロックを活用して、生徒の想像力や個性を伸ばし、表現力を高めるには、どう授業を展開していけばよいのかなど、国内外の事例をもとに考察なども行いました。
無限の可能性を持つレゴブロックを活用することで、生徒の「考える力」を育む授業のあり方を、教育に携わる多くの方との意見交換を通じて学ぶことができました。
受賞授業案「レゴのポッチを使った等差数列の導入」
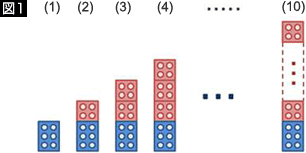
導入(図1):
(1)のように青いレゴをだけを見せ、次に赤レゴを1つ積み重ねて(2)を作る。もう1つレゴを積み重ねて順に積み重ねた時、(10)にあるポッチの数はいくつ?
ねらい:
ポッチを数えながら、その増え方やレゴの個数など数列の性質に気づかせる。
展開(図2):
ポッチ数の異なるレゴでも総数が計算できるよう、一般項を求めよう!
(1)のポッチの数をa1、積み重ねるポッチの数をdとすると、(1)のポッチ数はa1、(2)はa1+d、(3)はa1+2d…となり、n番目では a1+(n-1)dとなる。
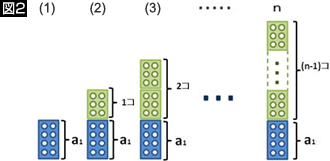
ポッチの総数:a1+(n-1)d
授業の展開:
ポッチの数が異なるレゴを選ぶことで、等比数列や階差数列、漸化式などにも応用可能。

